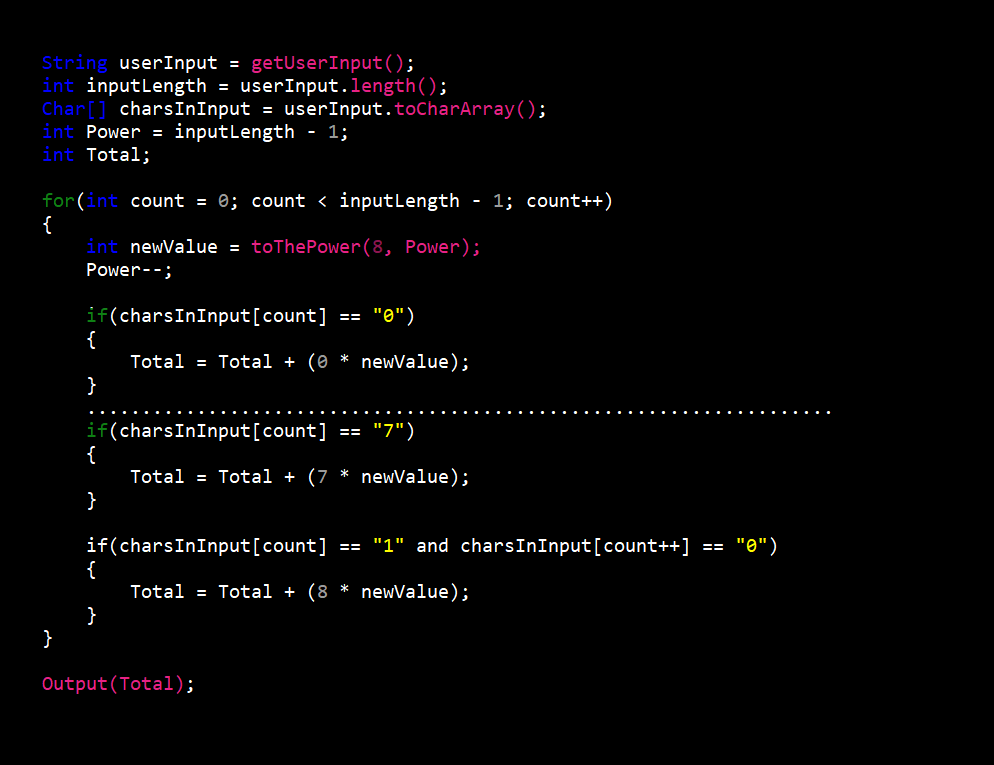
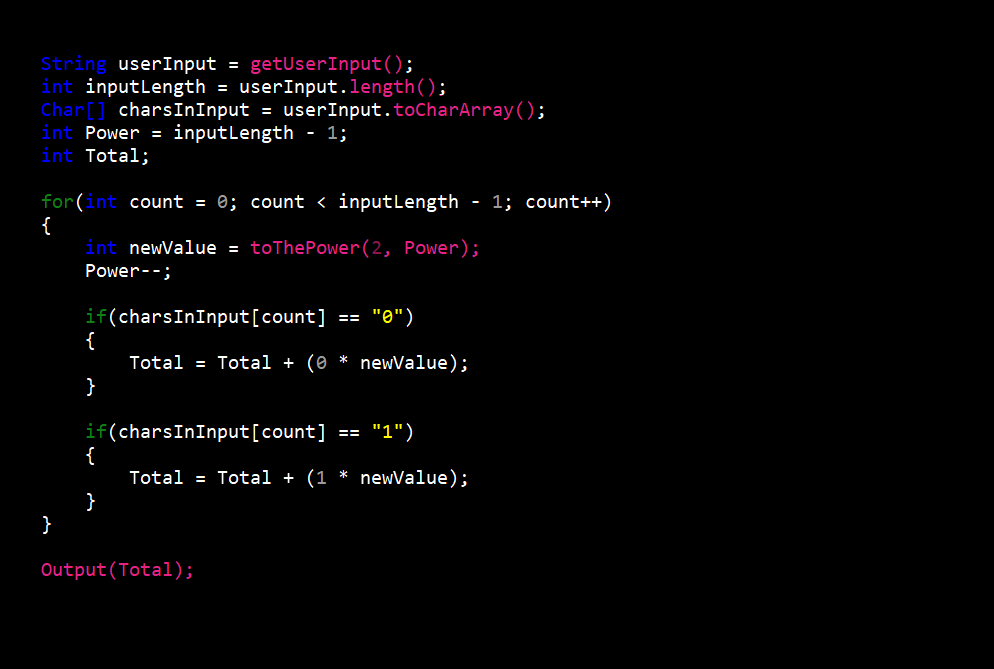
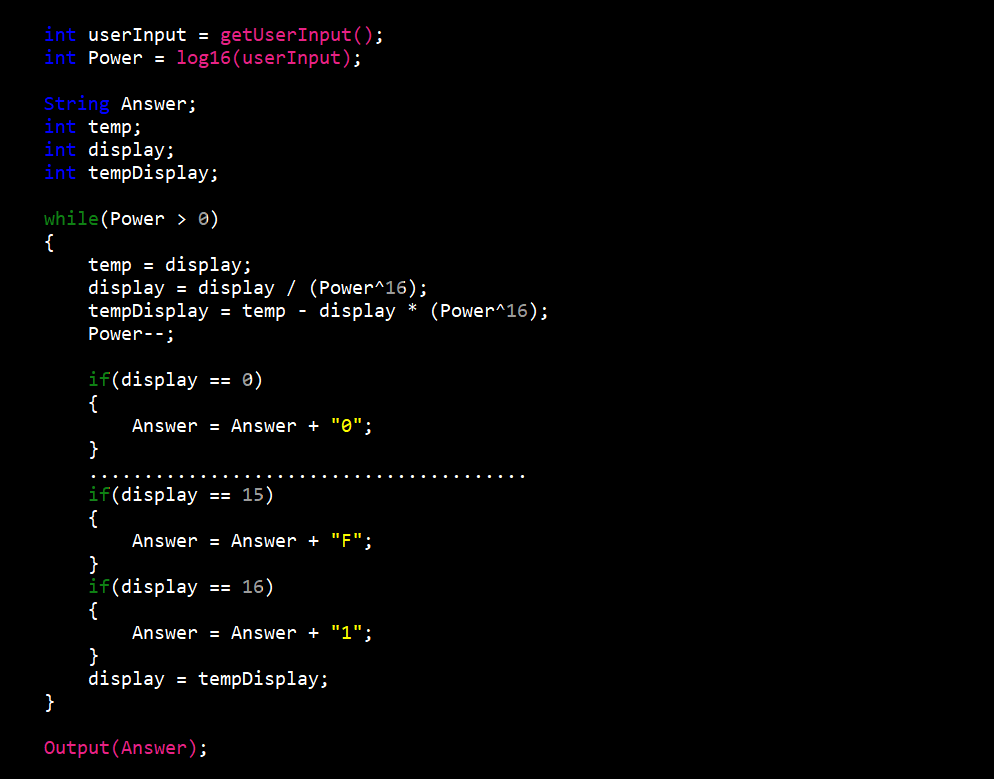
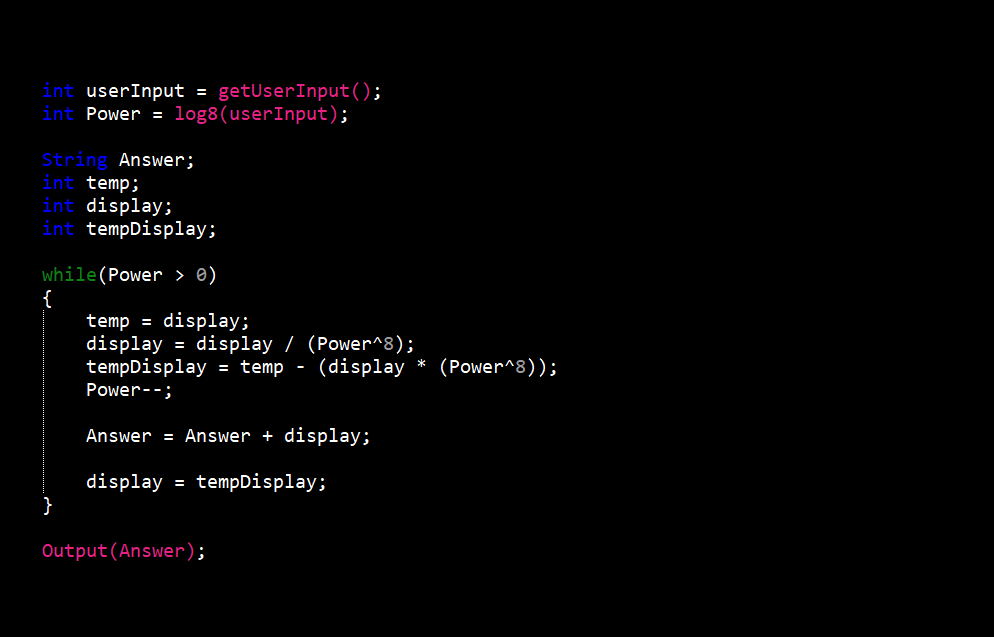
The hexadecimal to decimal converter was the most difficult of the six (6). I had to take into account fifteen (15) different character options when converting to decimal. Along with this, procedures also changed depending on the length of hexadecimal value entered.
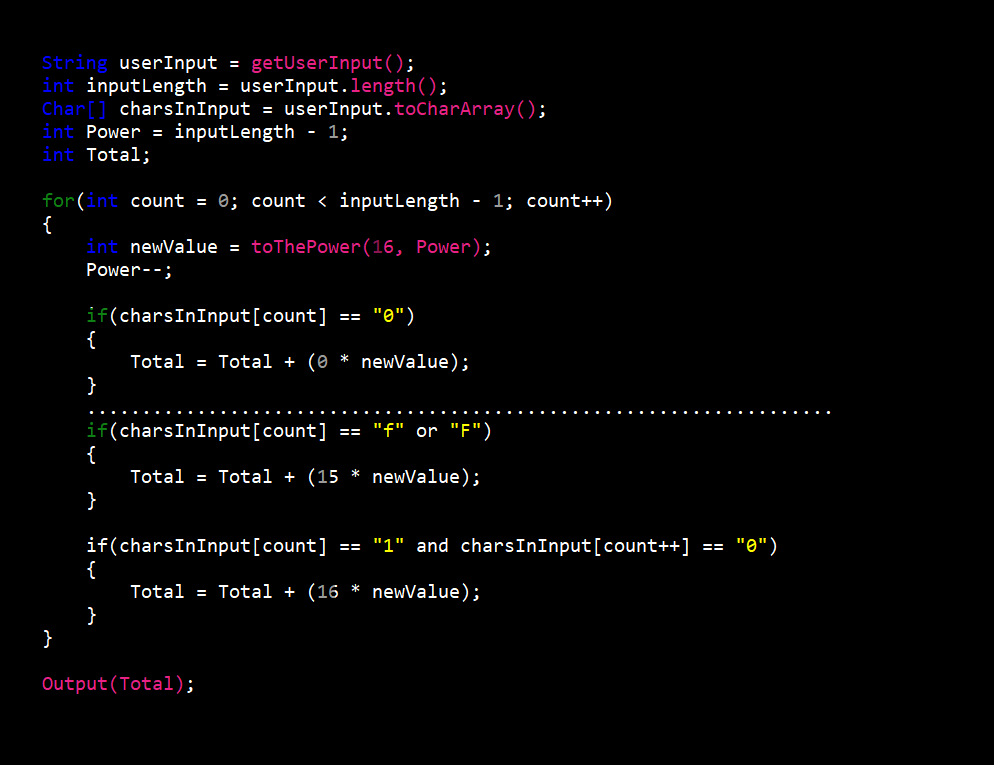
The procedure begins like the octal to decimal converter with getting the users input and as always when converting to decimal it is stored in a character array. Now if the input is more than one (1) character long, we take the first character and convert it to decimal (e.g. 3 equals 3 and f equals 15). We then take that number and multiply it by sixteen (16) to the power of the length of the input minus one (1) to give us a value we’ll call x. If the input were “30” this first step would give us 48 which since the only other character us “0”, x would be the final answer. If any other character is not “0” we would repeat this step and add the new value to x. If the input were “31” the final value would be 31 (3 = 48 and 1 = 1).
In the case of the input being only one character long the procedure is more simple. The only step is to convert the input value to decimal (e.g. 3 equals 3 and f equals 15) and this would be the final answer.